부자들이 자주하는 질문
Q1: 몬테카를로 시뮬레이션 결과가 실제 AI파워볼 승률에 어떻게 기여하나요?
A1: 무작위로 보일 수 있는 결과값들을 수만 번 반복 시행하여 특정 조건에서 승률이 극대화되는 구간을 통계적으로 찾아냅니다. 이는 단순한 추측이 아닌 수학적 확률 분포에 근거한 결정이므로 리스크를 현저히 낮춰줍니다.
Q2: 테더(USDT)의 움직임을 왜 파워볼 분석에 포함해야 하나요?
A2: 테더는 전 세계 재테크 자금의 유입량을 나타내는 선행 지표입니다. 자금의 유동성이 커지면 참여자의 심리 및 배당의 변화가 발생하며, AI는 이 정보를 확률 편차 분석에 반영하여 예측의 정교함을 더합니다.

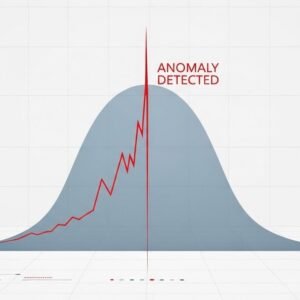
단순한 운에 의존하던 시대를 지나, 이제는 데이터 사이언스가 재테크 시장을 주도하고 있습니다. 그 중심에는 수만 번의 가상 시행을 통해 미래의 기댓값을 산출하는 몬테카를로 시뮬레이션 결과가 자리 잡고 있습니다. 특히 AI파워볼 시스템은 이러한 수학적 모델을 기반으로 테더(USDT) 자본의 이동 경로를 분석하여 그 어느 때보다 높은 예측 정확도를 보여주고 있습니다.
몬테카를로 시뮬레이션 결과가 갖는 기술적 가치
몬테카를로 방법은 무작위 샘플링을 반복하여 함수의 값을 추정하는 알고리즘입니다. AI파워볼에 이를 적용하면 발생 가능한 모든 경우의 수를 시뮬레이션하여 특정 구간에서 나타나는 패턴의 유의성을 검증할 수 있습니다. 이러한 확률적 접근법의 기초 이론은 위키백과 몬테카를로 방법 항목에서 상세히 연구해 볼 수 있습니다.
테더 유동성과 확률적 변동성 분석
디지털 자산 시장의 핵심 지표인 테더는 자본 유입의 척도입니다. 테더의 유동성이 급변할 때 AI파워볼의 결과값 분포 또한 미세한 변화를 보입니다. 성공적인 투자를 위해서는 단순한 결과값 추종이 아니라, 시스템 내부의 무결성 여부를 먼저 판단해야 합니다.

- 핵심 데이터: 가공되지 않은 통계의 힘 [무결성 데이터셋] 확인
- 오차 범위 점검: 표준 정규 분포를 활용한 [확률 편차 분석]
- 결과값 검증: 수만 회의 시행착오를 거친 [몬테카를로 시뮬레이션 결과] 활용
확률 편차 분석을 통한 리스크 관리
몬테카를로 시뮬레이션 결과가 보여주는 가장 큰 교훈은 일시적인 편차에 휘둘리지 말라는 것입니다. 확률 편차 분석을 통해 현재의 결과가 통계적 오차 범위 내에 있는지, 혹은 새로운 패턴의 시작인지를 구분해야 합니다. 테더의 대량 유입이 확인되는 시점과 AI 모델의 시뮬레이션 값이 일치할 때가 바로 가장 강력한 진입 타이밍이 됩니다.
결론: 수학적 모델이 만드는 압도적 수익 구조
결국 승리는 얼마나 정교한 모델을 가졌느냐에 달려 있습니다. 몬테카를로 시뮬레이션 결과와 테더 유동성 데이터를 결합한 AI파워볼은 인간의 직관을 넘어서는 과학적 재테크를 가능케 합니다. 무결성 데이터셋을 기반으로 한 확률 편차 분석을 통해 안정적인 수익의 길을 찾으시기 바랍니다.